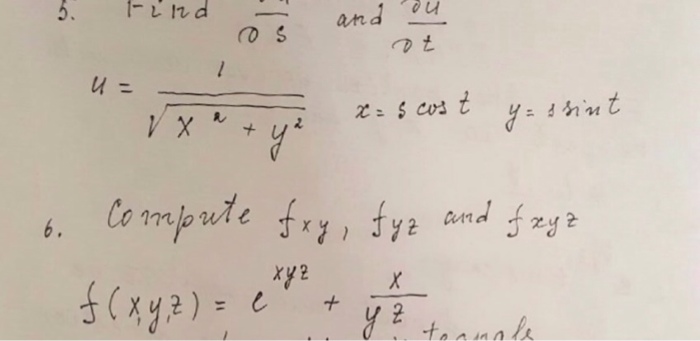
Solved Find Du Ds And Du Dt U 1 Square Root X 2 Y 2 X Chegg Com
Solve Problem $51$ in case sampling is without replacement As in $(a)$ and $(b)$ of Problem 51, $\mu=6$ and $\sigma^{2}=108, \theta=329$ (c) There are ${ }_{3} C_{2}=10$ samples of size two which can be drawn without replacement (this means that we draw one number and then another number different from the first) from the population, namelyIm Jahre 1733 zeigte Abraham de Moivre in seiner Schrift The Doctrine of Chances im Zusammenhang mit seinen Arbeiten am Grenzwertsatz für Binomialverteilungen eine Abschätzung des Binomialkoeffizienten, die als Vorform der Normalverteilung gedeutet werden kann Die für die Normierung der Normalverteilungsdichte zur Wahrscheinlichkeitsdichte notwendige Berechnung
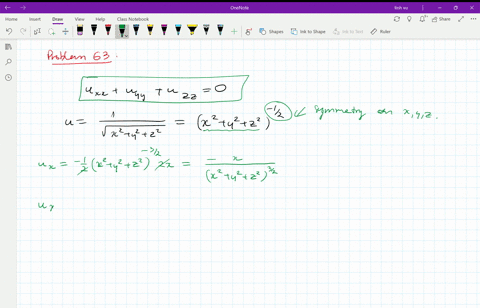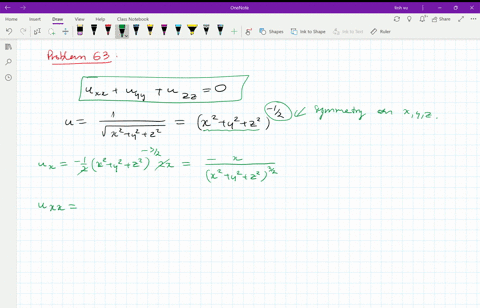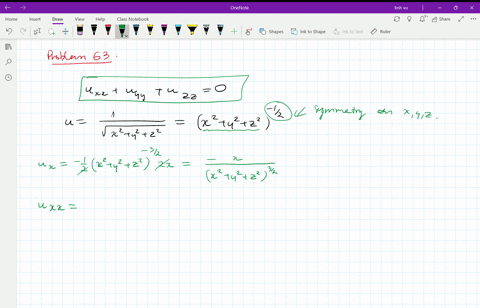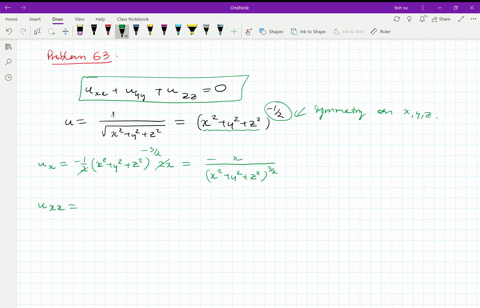
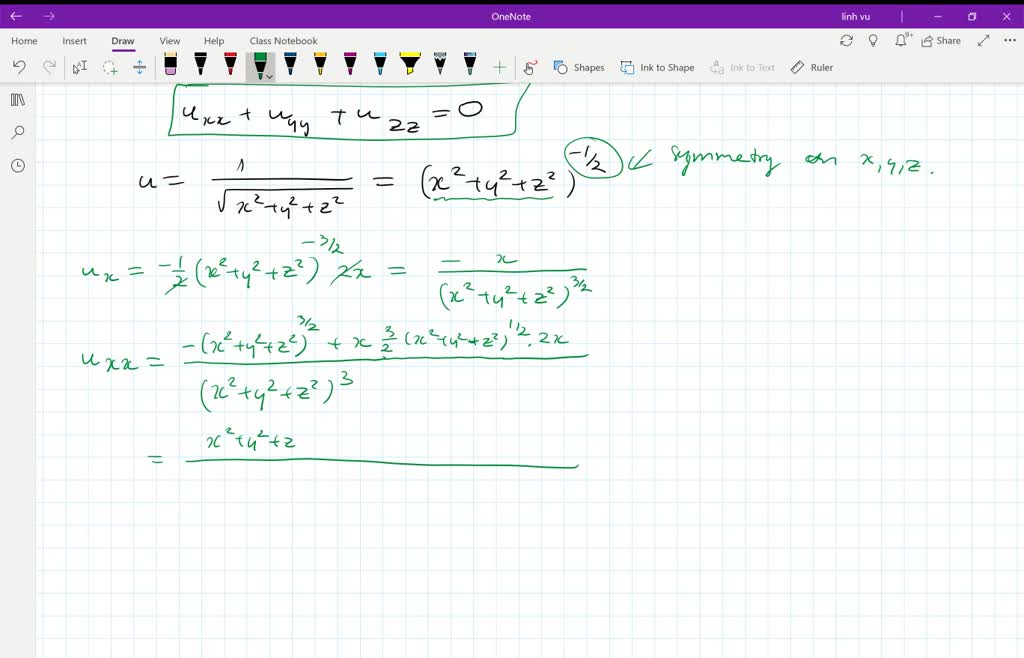
U=1/sqrt(x^2+y^2+z^2)
U=1/sqrt(x^2+y^2+z^2)-M11 Cálculo II Derivadas parciais Exercícios Derivadas parciais Selecione os exercícios por Dificuldade Fácil Médio Difícil Categoria Exercício Contextualizado Prática da Técnica Prática de Conceitos Demonstrações Problemas Complexos OutrosM11 Cálculo II Derivadas parciais Derivadas parciais Selecione os exercícios por Dificuldade Fácil Médio Difícil Categoria Exercício Contextualizado Prática da Técnica Prática de Conceitos Demonstrações Problemas Complexos Outros
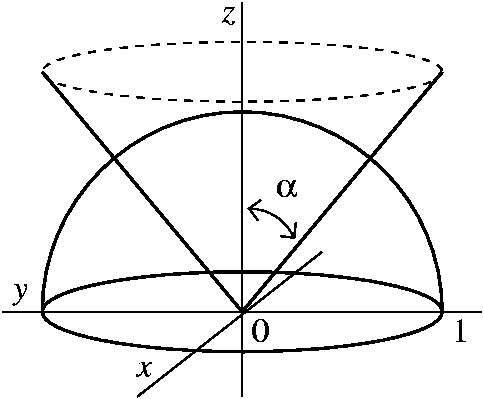
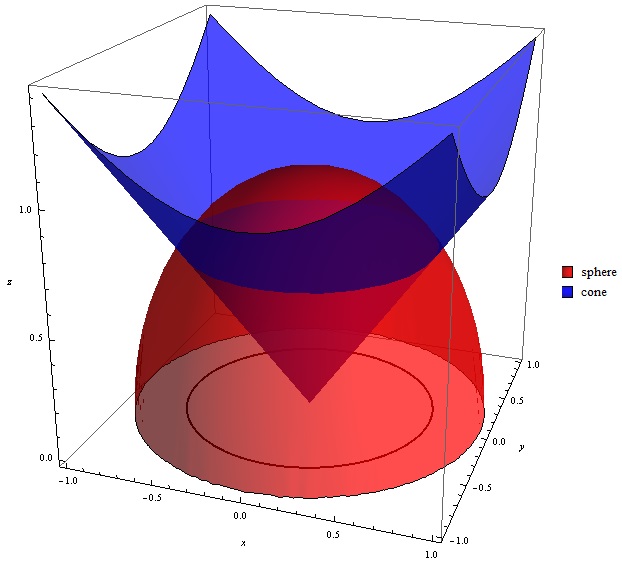
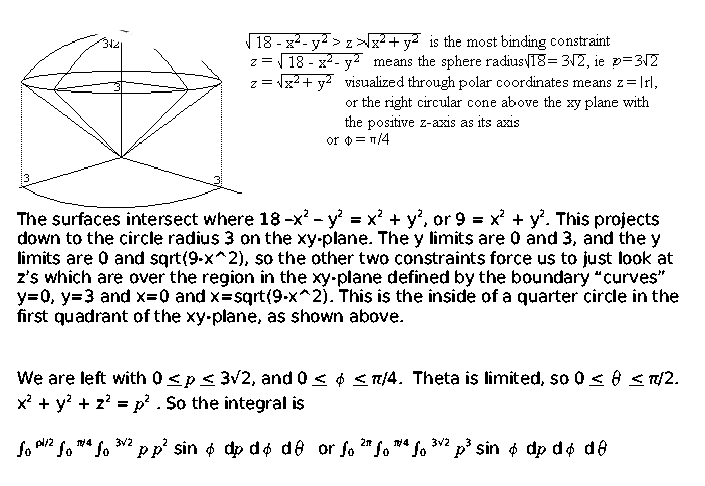
Answers To The Review Problems For The First Exam 251 05 10 In Spring 06
Cenni storici Sin dai tempi della matematica babilonese erano noti metodi risolutivi per equazioni di terzo grado particolari, essenzialmente quelle che possono essere ricondotte ad un'equazione di secondo gradoI greci riuscivano a risolvere alcune equazioni di terzo grado con il metodo delle coniche, metodo reso famoso dall'aneddoto della duplicazione dell'altare di Apollo
U=1/sqrt(x^2+y^2+z^2)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | 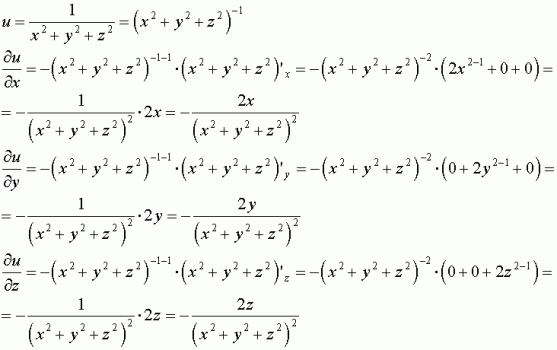 |  |
 | ||
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
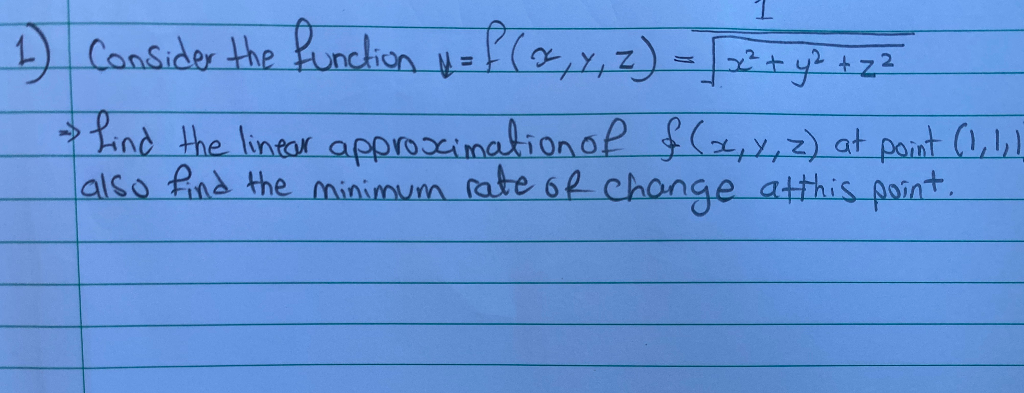 |  | |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 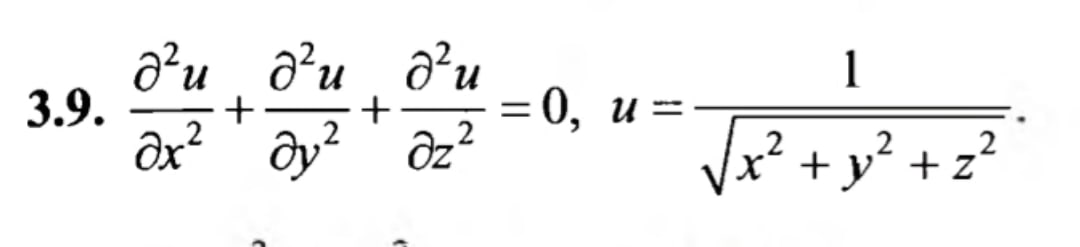 | |
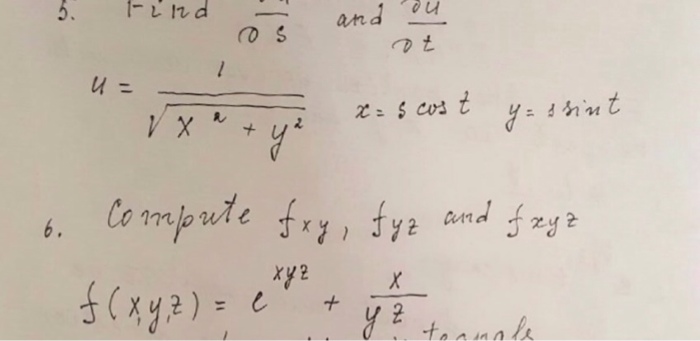 |  |  |
 |  | |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 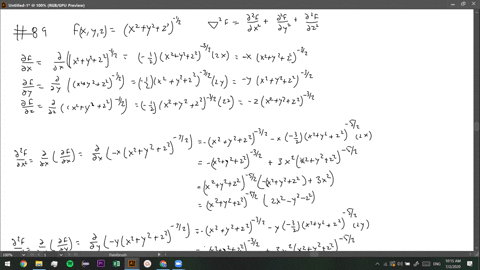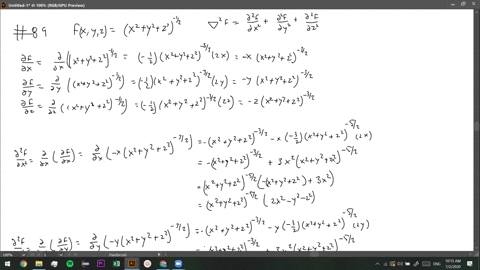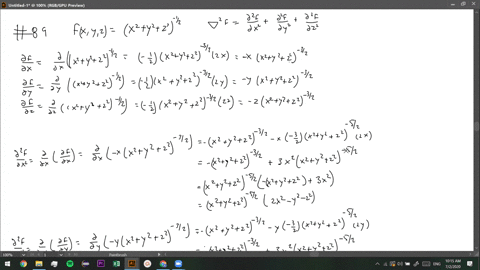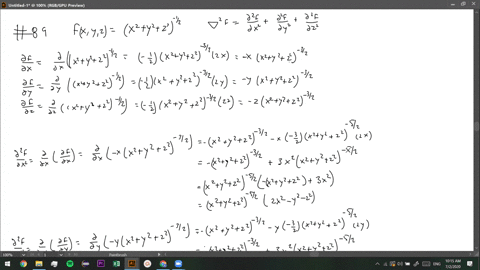 |  |
 |  | |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「U=1/sqrt(x^2+y^2+z^2)」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |





0 件のコメント:
コメントを投稿